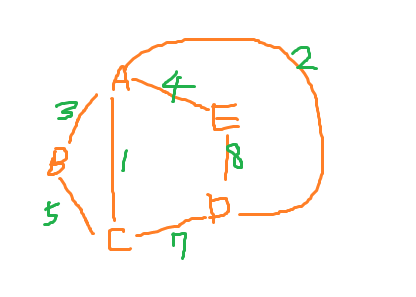
▶ 신장 트리(Spanning Tree) 그래프 내에 있는 모든 정점이 연결되어 있고 사이클이 없는 그래프 n개의 정점이 있다면 신장 트리의 간선 수는 n-1개가 된다 ▶ 최소 신장 트리 (Minimum Spanning Tree) 각 간선이 가지고 있는 가중치의 합이 최소가 되는 신장 트리 (가중치는 거리, 비용, 시간 등이 될 수 있다) 즉, 최소 신장 트리는 정점과 간선이 주어졌을 때, 최소 비용으로 정점들을 연결시키는 방법을 찾는 것이다. 이런 유형의 문제를 풀기 위해서는 프림 알고리즘(Prim’s Algorithm) 이나 크루스칼 알고리즘(Kruskal’s Algorithm) 을 사용해야한다. 사이클의 존재 유무를 확인할 때는 이전에 배웠던 유니온 find 방법을 이용하면 된다. Ex) A, B,..